19 Introduction to Spherical Harmonic Analysis
- Expansion of functions or observations in terms of spherical harmonics
- Mathematical background
- Application to global geophysical problems, e.g., the planetary magnetic field
- Modelling Earth’s global magnetic field
- Estimation of expansion coefficients from data
Spherical harmonic analysis is a mathematical method used extensively in geophysics to represent functions (based on observations) on the surface of a sphere. This technique is particularly useful for modeling the global geomagnetic field, which is inherently complex and varies both spatially and temporally.
In this chapter, we will cover the following topics:
- Legendre polynomials
- Solution of the Laplace equation in spherical coordinates
- Associated Legendre polynomials
- Schmidt quasi-normalized Legendre polynomials
Further, we emphasize the value of spherical harmonics in the mathematical description of the global magnetic field of the Earth.
19.1 Basics of Spherical Harmonics
Spherical harmonics are a set of orthogonal functions defined on the surface of a sphere. They are the spherical analogues of the Fourier series used in periodic functions. A spherical harmonic function\(Y_{n}^{m}(\theta, \phi) \in \mathbb C\) is defined by:
\[ Y_{n}^{m}(\theta, \phi) = \sqrt{\frac{(2n+1)(n-m)!}{4\pi(n+m)!}} P_{n}^{m}(\cos \theta) e^{im\phi} \]
where:
- \(n\) is the degree,
- \(m\) is the order,
- \(0 \le \theta \le \pi\) is the colatitude,
- \(0 \le \phi \le 2 \pi\) is the longitude,
- \(P_{n}^{m}(\cos\theta)\) are the associated Legendre polynomials.
19.1.1 Application to the Global Geomagnetic Field
The Earth’s magnetic field can be expressed as a potential field, which is the gradient of a scalar potential \(V\). This potential can be expanded in terms of spherical harmonics:
\[ V(r, \theta, \phi) = a \sum_{n=1}^{\infty} \left( \frac{a}{r} \right)^{n+1} \sum_{m=0}^{n} \left( g_{n}^{m} \cos m\phi + h_{n}^{m} \sin m\phi \right) P_{n}^{m}(\cos \theta) \]
where:
- \(a\) is the Earth’s mean radius,
- \(r\) is the radial distance from the Earth’s center,
- \(g_{n}^{m}\) and \(h_{n}^{m}\) are the Gauss coefficients, which are determined from observations.
19.1.2 Importance in Geophysics
- Global Representation: Spherical harmonics provide a global representation of the geomagnetic field, allowing for the analysis of its spatial variations.
- Data Fitting: By fitting observational data to a spherical harmonic model, geophysicists can infer the distribution of magnetic sources within the Earth.
- Temporal Changes: The coefficients \(g_{n}^{m}\) and \(h_{n}^{m}\) can be monitored over time to study secular variation, which is the slow change in the Earth’s magnetic field.
19.1.3 Challenges and Considerations
- Resolution: The degree \(n\) determines the resolution of the model; higher degrees provide more detail but require more data and computational power.
- Data Quality: Accurate spherical harmonic models depend on high-quality, globally distributed magnetic field measurements.
19.2 Example
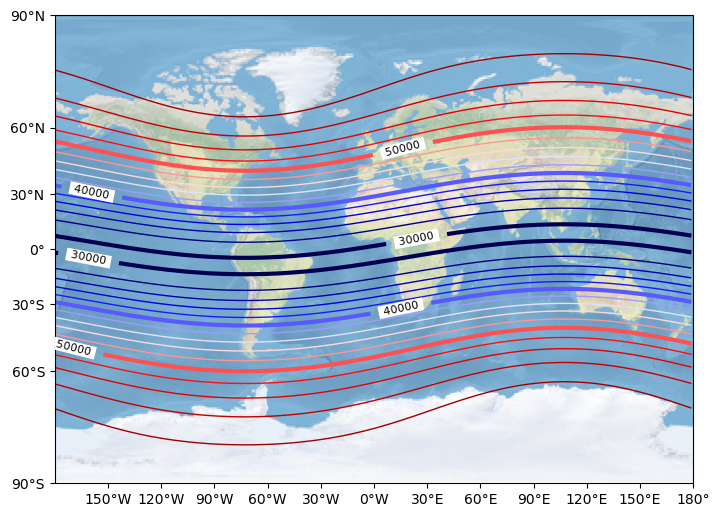
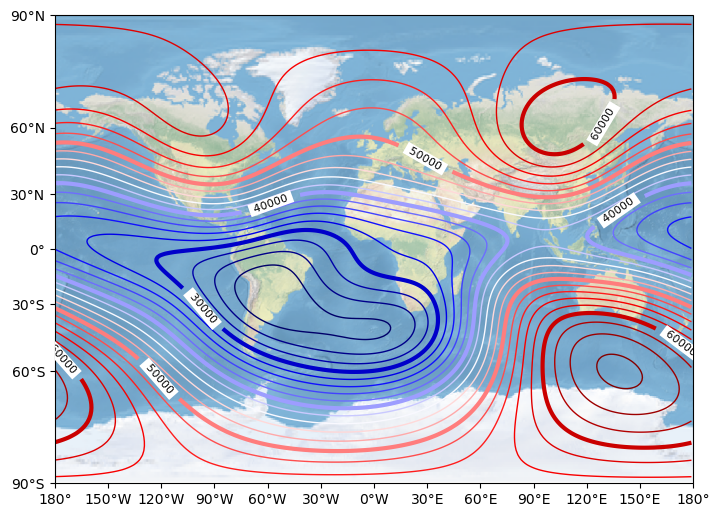
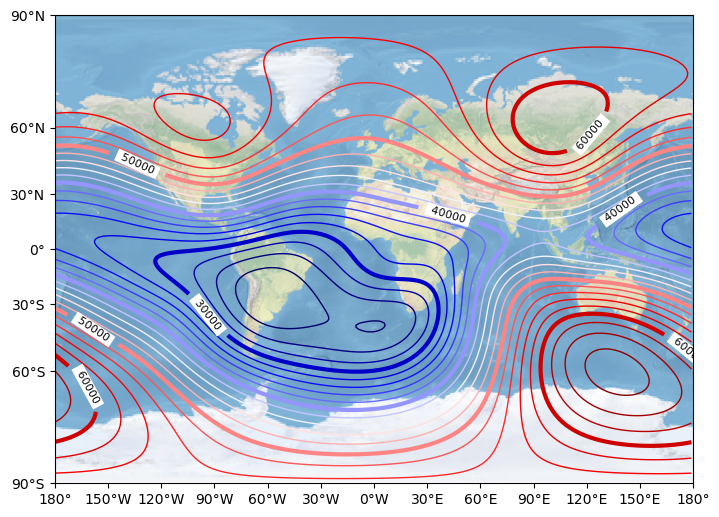
The following figures illustrate the Earth’s total magnetic field (in nT) computed from the 15th generation of the International Geomagnetic Reference Field (IGRF) model. From left to right, the spherical harmonic degree \(n\) increases from 1 to 6 and then to 13.
For \(n=1\), the field exhibits a dipolar structure whose dipole axis is inclined relative to the Earth’s rotation axis. For degrees greater than 1, higher-order multipole contributions are present.