23 Mathematical description of the Earth’s global magnetic field
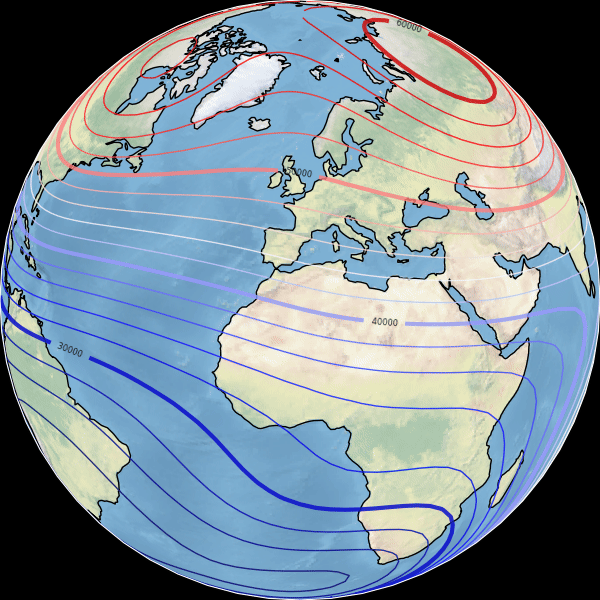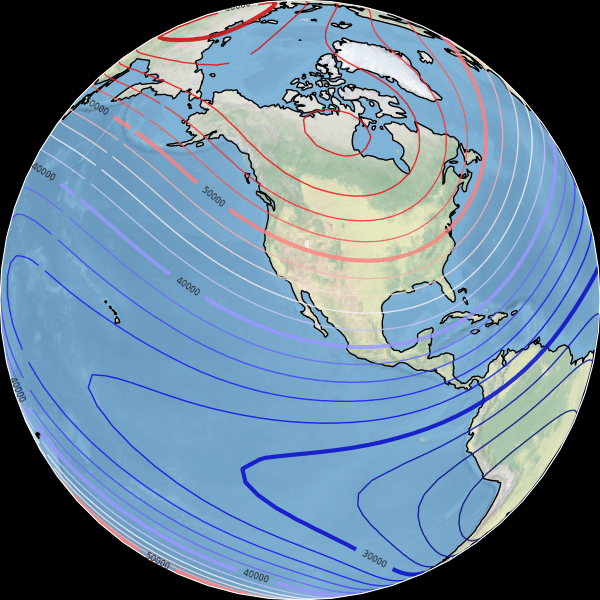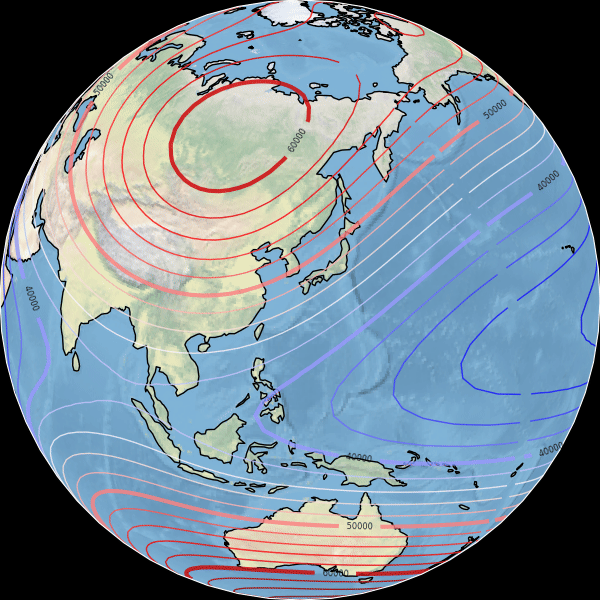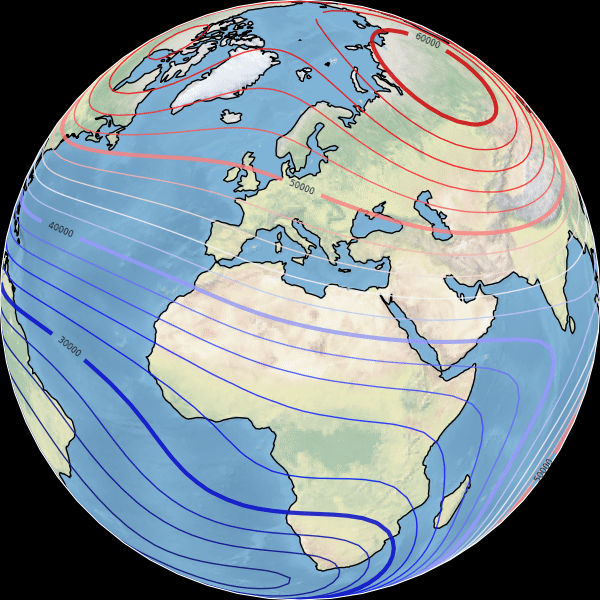
The goal of this section is to describe the main geomagnetic field \(\vb B(r, \theta, \varphi, t)\) produced primarily by internal sources inside Earth’s core.
The description in terms of a potential is valid on and above Earth’s surface, where the main magnetic field can be represented by the gradient of a scalar function, i.e., \(\vb B = -\grad V\).
The potential function \(V(r, \theta, \varphi, t)\) is represented as a finite series expansion in terms of spherical harmonic coefficients, \(g_n^m\) and \(h_n^m\), also known as Gauss coefficients:
\[ V(r, \theta, \varphi, t) = a \sum\limits_{n=1}^N \sum\limits_{m=0}^n \left( \frac{a}{r} \right)^{n+1} \left[ g_n^m(t) \cos m \varphi + h_n^m(t) \sin m \varphi \right] P_n^m(\cos\theta). \tag{23.1}\]
Here, \(r, \theta\) and \(\varphi\) refer to coordinates in a geocentric spherical coordinate system with \(r\) being the radial distance from the center of the Earth, and \(\theta, \varphi\) being geocentric co-latitude and longitude, resp.
As reference radius, the approximate mean radius of the Earth of \(a=6371.2\) km is chosen. The factor \(a^{n+2}\) is chosen so that the Gauss coefficients will have units of magnetic flux density.
The \(P_n^m(\cos\theta)\) are Schmidt semi-normalized associated Legendre functions of degree \(n\) and order \(m\).
The parameter \(N\) specifies the maximum spherical harmonic degree of expansion.
The Gauss coefficients change in time.
23.1 The geomagnetic components
The magnetic field on or above the Earth is usually described in terms of its Cartesian components \(X, Y\) and \(Z\).
The coordinate system is oriented such that \(X\) is pointing towards true magnetic North, \(Y\) is pointing eastwards, \(Z\) is pointing downwards.
The projection of the magnetic field line onto the horizontal plane tangential to the Earth’s surface is called \(H\). The angle between \(H\) and true North is referred to as magnetic declination.
The geomagnetic field of internal origin is
\[ \vb B(r, \theta, \varphi) = -\pdv{V}{r}\vb e_r - \frac{1}{r}\pdv{V}{\theta}\vb e_\theta -\frac{1}{r \sin\theta} \pdv{V}{\varphi}\vb e_\varphi, \]
in which \(\vb e_r\), \(\vb e_\theta\), \(\vb e_\varphi\) are unit vectors in spherical coordinates.
The following table shows the relation between the field components in Cartesian and spherical coordinates:
| \(\mathbf B(x,y,z)=\) | \(\mathbf B(r, \varphi, \theta)=\) | \(-\nabla V=\) |
|---|---|---|
| \(X \mathbf e_x\) | \(-B_\theta \mathbf e_\theta\) | \(+\dfrac{1}{r}\dfrac{\partial V}{\partial \theta}\mathbf e_\theta\) |
| \(Y \mathbf e_y\) | \(+B_\varphi \mathbf e_\varphi\) | \(-\dfrac{1}{r \sin\theta}\dfrac{\partial V}{\partial \varphi}\mathbf e_\varphi\) |
| \(Z \mathbf e_z\) | \(-B_r \mathbf e_r\) | \(+\dfrac{\partial V}{\partial r}\mathbf e_r\) |
For the components in spherical coordinates we find
\[ B_r = -Z = -\frac{\partial V}{\partial r} =+\sum_{n=1}^{\infty} \sum_{m=0}^{n}(n+1) \left( \frac{a}{r}\right)^{n+2} \left[g_{n}^{m} \cos m \varphi+h_{n}^{m} \sin m \varphi\right] P_{n}^{m}(\cos \theta) \]
\[ B_\theta = -X = -\frac{1}{r}\dfrac{\partial V}{\partial \theta} = -\sum_{n=1}^{\infty} \sum_{m=0}^{n}\left( \frac{a}{r} \right)^{n+2} \left[g_{n}^{m} \cos m \varphi+h_{n}^{m} \sin m \varphi\right] \frac{\partial P_{n}^{m}(\cos \theta)}{\partial \theta} \]
\[ B_\varphi = +Y = -\frac{1}{r \sin\theta}\dfrac{\partial V}{\partial \varphi} =-\sum_{n=1}^{\infty} \sum_{m=0}^{n}\left( \frac{a}{r} \right)^{n+2}\left[-g_{n}^{m} \sin m \varphi+h_{n}^{m} \cos m \varphi\right] \frac{1}{\sin \theta} P_{n}^{m}(\cos \theta) \]
23.2 The International Geomagnetic Reference Field (IGRF)
Link to the Gauss coefficients and general information about the 14th generation of the IGRF is here.
The IGRF provides Gauss coefficients \(g_n^m, h_n^m\) and their respective time derivatives \(\dot{g}_n^m, \dot{h}_n^m\) (in units of nT and nT/year, resp.) for a truncated spherical harmonic expansion up to degree \(N=13\). The IGRF is valid for a 5-year interval referred to as epoch.
The Gauss coefficients have a linear time dependency valid for one epoch. In the case of IGRF-14, the epoch starts with Jan 1st, 2025, and ends Jan 1st, 2030. Starting from \(T_0=2025\), we can extrapolate
\[ g_n^m(t) = g_n^m(T_0) + \dot{g}_n^m(T_0)(t - T_0) \] and \[ h_n^m(t) = h_n^m(T_0) + \dot{h}_n^m(T_0)(t - T_0). \]
23.3 The dipole field
The first three Gauss coefficients \(g_1^0, g_1^1, h_1^1\) can be used to calculate the contribution to the dipole field of the Earth.
From the IGRF-14, we get
| g/h | n | m | coeff. in nT |
|---|---|---|---|
| g | 1 | 0 | -29350.0 |
| g | 1 | 1 | -1410.3 |
| h | 1 | 1 | 4545.5 |
We see from 23.1, that for \(n=1\) we can write the dipole potential as
\[ V^D(r, \theta, \varphi) = \frac{a^3}{r^2} \left[ g_1^0 P_1^0(\cos\theta) + (g_1^1 \cos\varphi + h_1^1 \sin\varphi)P_1^1(\cos\theta) \right]. \]
Note that
\[ P_1^0(\cos\theta) = \cos\theta, \quad P_1^1(\cos\theta) = \sin\theta, \]
which yields
\[ V_D = \frac{a^3}{r^2} \left[ g_1^0 \cos\theta + g_1^1 \cos\varphi \sin\theta + h_1^1 \sin\varphi \sin\theta \right]. \]
Change from spherical to Cartesian coordinates gives
\[ V^D = \frac{a^3}{r^2} \left[ g_1^0 \frac{z}{r} + g_1^1 \frac{x}{r} + h_1^1 \frac{y}{r} \right]. \]
We compare this result with the well-known potential for a magnetic dipole with dipole moment \(\vb m = [m_x, m_y, m_z]^\top\):
\[ \begin{align} V & = \frac{\mu_0}{4 \pi } \frac{\vb m \cdot \vb e_r}{r^2} \\ & = \frac{\mu_0}{4 \pi r^{2}} \left[ m_x \frac{x}{r} + m_y \frac{y}{r} + m_z \frac{z}{r} \right] \end{align} \]
We identify, e.g., that
\[ \frac{a^3}{r^2}g_1^0 = \frac{\mu_0}{4 \pi r^{2}} m_z, \]
which enables us to calculate the magnetic dipole moment of the Earth in units of A\(\cdot\)m\(^2\) component-wise:
\[ \begin{align} m_x & = \frac{4 \pi}{\mu_0} a^3 g_1^1 = -0.37 \times 10^{22} \\ m_y & = \frac{4 \pi}{\mu_0} a^3 h_1^1 = 1.18 \times 10^{22} \\ m_z & = \frac{4 \pi}{\mu_0} a^3 g_1^0 = -7.59 \times 10^{22} \end{align} \]
The magnititude of the dipole moment is \(m = 7.69 \times 10^{22}\) A\(\cdot\)m\(^2\).
From the components of the dipole moment we can infer the axis of the dipole in terms of the angles of orientation.
We get
\[ \theta_S = \arccos\frac{m_z}{m} = 170.7\textdegree \] and \[ \varphi_S = \arccos\frac{m_x}{\sqrt{m_x^2 + m_y^2}} = 107.4\textdegree. \]
This refers to the point where the dipole axis intersects the surface of the Earth ain the southern hemisphere. In the northern hemisphere, we have
\[ \theta_N = 9.3\textdegree \text{ and } \varphi_N = 72.6\textdegree. \]
We refer to these points as the geomagnetic pole.
The magnetic poles are located at the points where the observed magnetic field is purely vertical with respect to the surface of the Earth, i.e., where we observe \(H=0\) and an inclination angle of 90\(\textdegree\).
23.4 Estimation of the Gauss coefficients
In the spherical harmonics expansion 23.1, the Gauss coefficients appear as linear coefficients.
Given suffiently many observations of the field components, the coefficients can be estimated using the Method of Least Squares.