Code
using JSServe: Page # hide
Page(exportable=true, offline=true) # hideWas die Analyse von Plasmen besonders schwierig macht, ist die Tatsache, dass die Dichten in einem Zwischenbereich liegen. Flüssigkeiten wie Wasser sind so dicht, dass die Bewegungen der einzelnen Moleküle nicht berücksichtigt werden müssen. Es dominieren Kollisionen, und die einfachen Gleichungen der gewöhnlichen Flüssigkeitsdynamik reichen aus. Im anderen Extremfall, in Geräten mit sehr geringer Dichte, müssen nur die Flugbahnen einzelner Teilchen berücksichtigt werden; kollektive Effekte sind oft unwichtig. Ein Plasma verhält sich manchmal wie eine Flüssigkeit und manchmal wie eine Ansammlung von Einzelteilchen. Der erste Schritt, um zu lernen, wie man mit dieser schizophrenen Persönlichkeit umgeht, besteht darin zu verstehen, wie sich einzelne Teilchen in elektrischen und magnetischen Feldern verhalten.
Hier gehen wir davon aus, dass die EM-Felder vorgegeben sind und nicht von den geladenen Teilchen beeinflusst werden. Die Materialien hier lehnen sich eng an F.F.Chens Einführung in die Plasmaphysik und kontrollierte Fusion an.
In allen Beispielen gehen wir davon aus, dass die folgenden Pakete geladen sind:
using JSServe: Page # hide
Page(exportable=true, offline=true) # hideusing TestParticle
using TestParticle: get_gc
using TestParticleMakie
using OrdinaryDiffEq
using StaticArrays
using LinearAlgebra
import GLMakie as WMIn diesem Fall führt ein geladenes Teilchen eine einfache Gyrationsbewegung aus. Die Bewegungsgleichung lautet
\[ m\frac{\mathrm d\mathbf{v}}{\mathrm dt} = q\mathbf{v}\times\mathbf{B} \]
Nimmt man \(\widehat{z}\) als die Richtung von \(\mathbf{B}\) (\(\mathbf{B} = B\widehat{z}\)), so gilt
\[ \begin{aligned} m\dot{v}_x = qB v_y,\, m\dot{v}_y = -qB v_x,\, m\dot{v}_z = 0, \\ \ddot{v}_x = \frac{qB}{m}\dot{v}_y = -\big( \frac{qB}{m}\big)^2 v_x \\ \ddot{v}_y = \frac{qB}{m}\dot{v}_x = -\big( \frac{qB}{m}\big)^2 v_y \end{aligned} \]
Dies beschreibt einen einfachen harmonischen Oszillator mit der Gyrationsfrequenz, die wir wie folgt definieren
\[ \omega_c \equiv \frac{| q | B}{m} \]
Nach der von uns gewählten Konvention ist \(\omega_c\) immer nicht-negativ. Die Lösung für die Geschwindigkeit ist dann
\[ v_{x,y} = v_\perp \exp(\pm i \omega_c t + i\delta_{x,y}) \]
Die \(\pm\) bezeichnen das Vorzeichen von q. Wir können die Phase \(\delta\) so wählen, dass
\[ v_x = v_\perp e^{i\omega_c t} = \dot{x} \]
wobei \(v_\perp\) eine positive Konstante ist, die die Geschwindigkeit in der Ebene senkrecht zu \(\mathbf{B}\) angibt. Dann gilt
\[ v_y = \frac{m}{qB} \dot{v}_x = \pm \frac{1}{\omega_c}\dot{v}_x = \pm i v_\perp e^{i\omega_c t} = \dot{y} \]
Nochmalige Integration liefert
\[ \begin{aligned} x - x_0 &= -i\frac{v_\perp}{\omega_c}e^{i\omega_c t} \\ y - y_0 &= \pm i\frac{v_\perp}{\omega_c}e^{i\omega_c t} \end{aligned} \]
Wir definieren die Gyrationsradius zu
\[ r_L \equiv \frac{v_\perp}{\omega_c} = \frac{mv_\perp}{|q| B} \]
Der Realteil liefert
\[ \begin{aligned} x - x_0 &= r_L\sin\omega_c t \\ y - y_0 &= \pm r_L \cos\omega_c t \end{aligned} \]
Diese beschreibt eine Kreisbahn um ein Führungszentrum (\(x_0, y_0\)), das ortsfest ist. Die Richtung der Kreisbewegung ist immer so, dass das von dem geladenen Teilchen erzeugte Magnetfeld dem von außen angelegten Feld entgegengesetzt ist. Plasmateilchen neigen daher dazu, das Magnetfeld zu schwächen, und Plasmen sind diamagnetisch. Zusätzlich zu dieser Bewegung gibt es eine beliebige Geschwindigkeit \(v_z\) entlang \(\mathbf{B}\), die von \(\mathbf{B}\) nicht beeinflusst wird. Die Flugbahn eines geladenen Teilchens im Raum ist im Allgemeinen eine Spirale.
function uniform_B(x)
return SA[0.0, 0.0, 1e-8]
end
function uniform_E(x)
return SA[0.0, 0.0, 0.0]
end
x0 = [1.0, 0, 0]
v0 = [0.0, 1.0, 0.1]
stateinit = [x0..., v0...]
tspan = (0, 18)
param = prepare(uniform_E, uniform_B, species=Proton)
prob = ODEProblem(trace!, stateinit, tspan, param)
sol = solve(prob, Tsit5(); save_idxs=[1,2,3,4,5,6])
WM.plot(sol)
Wenn wir nun ein elektrisches Feld zulassen, ergibt sich die Bewegung als Summe zweier Bewegungen: die kreisförmige Gyration und eine Drift des Führungszentrums. Wir können \(\mathbf{E}\) so wählen, dass es in der Ebene \(x\)-\(z\) liegt, so dass \(E_y = 0\) ist. Wie zuvor ist die \(z\)-Komponente der Geschwindigkeit unabhängig von den transversalen Komponenten und kann separat behandelt werden. Die Bewegungsgleichung lautet nun
\[ m\frac{d\mathbf{v}}{dt} = q( \mathbf{E} + \mathbf{v}\times\mathbf{B} ) \]
dessen \(z\)-Komponente lautet
\[ \frac{dv_z}{dt} = \frac{q}{m}E_z \]
oder
\[ v_z = \frac{qE_z}{m}t + v_{z0} \]
Dies ist eine einfache Beschleunigung entlang \(\mathbf{B}\). Die Komponenten senkrecht dazu sind
\[ \begin{aligned} \frac{dv_x}{dt} &= \frac{q}{m}E_x \pm \omega_c v_y \\ \frac{dv_y}{dt} &= 0 \mp \omega_c v_x \end{aligned} \]
Nach Differentiation bei konstantem elektrischen Feld erhalten wir
\[ \begin{aligned} \ddot{v}_x &= -\omega_c^2 v_x \\ \ddot{v}_y &= \mp \omega_c \Big( \frac{q}{m}E_x \pm \omega_c v_y \Big) = -\omega_c^2 \Big( v_y + \frac{E_x}{B} \Big) \end{aligned} \]
welches wir umschreiben
\[ \frac{d^2}{dt^2}\Big( v_y + \frac{E_x}{B} \Big) = -\omega_c^2\Big( v_y + \frac{E_x}{B} \Big) \]
so dass es sich auf den vorherigen Fall reduziert, wenn wir \(v_y\) durch \(v_y + (E_x/B)\) ersetzen. Die Geschwindigkeitslösung wird dann ersetzt durch
\[ \begin{aligned} v_x &= v_\perp e^{i\omega_c t} \\ v_y &= \pm v_\perp e^{i\omega_c t} - \frac{E_x}{B} \end{aligned} \]
Die Gyrationsbewegung ist dieselbe wie zuvor, aber es wird eine Drift \(\mathbf{v}_{gc}\) des Führungszentrums in negative y-Richtung (für \(E_x > 0\)) überlagert.
Um eine allgemeine Formel für \(\mathbf{v}_{gc}\) zu erhalten, können wir die Impulsgleichung in Vektorform lösen. Wir können den Term \(m d\mathbf{v}/dt\) weglassen, da dieser Term nur die Kreisbewegung bei \(\omega_c\) ergibt, die wir bereits kennen. Die Impulsgleichung lautet dann
\[ \mathbf{E} + \mathbf{v}\times\mathbf{B} = 0 \]
Nimmt man das Kreuzprodukt mit \(\mathbf{B}\), so erhält man
\[ \mathbf{E}\times\mathbf{B} = \mathbf{B}\times(\mathbf{v}\times\mathbf{B}) = \mathbf{v}B^2 - \mathbf{B}(\mathbf{v}\cdot\mathbf{B}) \]
Die zum Magnetfeld transversale Komponente dieser Gleichung lautet
\[ \mathbf{v}_{gc} = \mathbf{E}\times\mathbf{B}/B^2 \equiv \mathbf{v}_E \]
Wir definieren dies als \(\mathbf{v}_E\), die durch das elektrische Feld verursachte Drift des Führungszentrums. Der Größenordnung nach ist diese Drift
\[ v_E = \frac{E(\text{V/m})}{B(\text{tesla})}\frac{\text{m}}{\text{sec}} \]
Es ist wichtig zu beachten, dass \(\mathbf{v}_E\) unabhängig von q, m und \(v_\perp\) ist. Der Grund dafür ergibt sich aus dem folgenden physikalischen Bild. Im ersten Halbzyklus der Ionenbahn gewinnt das Ion Energie aus dem elektrischen Feld und erhöht \(v_\perp\) und damit auch \(r_L\). Im zweiten Halbzyklus verliert es Energie und nimmt in \(r_L\) ab. Dieser Unterschied in \(r_L\) auf der linken und rechten Seite der Bahn verursacht die Drift \(v_E\). Ein negatives Elektron dreht sich in die entgegengesetzte Richtung, gewinnt aber auch Energie in die entgegengesetzte Richtung; es driftet schließlich in dieselbe Richtung wie ein Ion. Bei Teilchen mit gleicher Geschwindigkeit, aber unterschiedlicher Masse, hat das leichtere Teilchen ein kleineres \(r_L\) und driftet daher weniger pro Zyklus. Allerdings ist auch seine Gyrationsfrequenz größer, und die beiden Effekte heben sich genau auf. Zwei Teilchen mit gleicher Masse, aber unterschiedlicher Energie hätten das gleiche \(\omega_c\). Das langsamere Teilchen hat ein kleineres \(r_L\) und gewinnt daher weniger Energie aus \(\mathbf{E}\) in einem Halbzyklus. Bei weniger energiereichen Teilchen ist jedoch der Anteil der \(r_L\)-Änderung bei einer gegebenen Energieänderung größer, und diese beiden Effekte heben sich auf.
Die dreidimensionale Umlaufbahn im Raum ist also eine schräge Helix mit wechselnder Steigung.
function uniform_B(x)
return SA[0, 0, 1e-8]
end
function uniform_E(x)
return SA[1e-9, 0, 0]
end
# trace the orbit of the guiding center
function trace_gc!(dx, x, p, t)
_, _, E, B, sol = p
xu = sol(t)
Bv = B(x)
b = normalize(Bv)
v_par = (xu[4:6]⋅b).*b
B2 = sum(Bv.^2)
dx[1:3] = (E(x)×Bv)/B2 + v_par
end
x0 = [1.0, 0, 0]
v0 = [0.0, 1.0, 0.1]
stateinit = [x0..., v0...]
tspan = (0, 20)
# E×B drift
param = prepare(uniform_E, uniform_B, species=Proton)
prob = ODEProblem(trace!, stateinit, tspan, param)
sol = solve(prob, Tsit5(); save_idxs=[1,2,3,4,5,6])
gc = get_gc(param)
gc_x0 = [gc_i(stateinit) for gc_i in gc]
prob_gc = ODEProblem(trace_gc!, gc_x0, tspan, (param..., sol))
sol_gc = solve(prob_gc, Tsit5(); save_idxs=[1,2,3])
gc_analytic = Tuple(xu -> getindex(sol_gc(xu[7]), i) for i = 1:3)
# numeric result and analytic result
orbit(sol, vars=[(1, 2, 3), gc, gc_analytic])
Das vorherige Ergebnis kann auf andere Kräfte übertragen werden, indem \(q\mathbf{E}\) in der Bewegungsgleichung durch eine allgemeine Kraft \(\mathbf{F}\) ersetzt wird. Die durch \(\mathbf{F}\) verursachte Drift des Führungszentrums ist dann
\[ \mathbf{v}_f = \frac{1}{q}\frac{\mathbf{F}\times\mathbf{B}}{B^2} \]
Insbesondere wenn \(\mathbf{F}\) die Schwerkraft \(m\mathbf{g}\) ist, gibt es eine Drift
\[ \mathbf{v}_g = \frac{m}{q}\frac{\mathbf{g}\times\mathbf{B}}{B^2} \]
Sie ähnelt der Drift \(\mathbf{v}_E\) insofern, als sie sowohl zur Kraft als auch zu \(\mathbf{B}\) senkrecht steht, unterscheidet sich aber in einem wichtigen Punkt. Die Drift \(\mathbf{v}_g\) ändert ihr Vorzeichen mit der Ladung des Teilchens. Unter einer Gravitationskraft driften Ionen und Elektronen in entgegengesetzte Richtungen, so dass sich im Plasma eine Nettostromdichte ergibt, die durch
\[ \mathbf{j} = n(M+m)\frac{\mathbf{g}\times\mathbf{B}}{B^2} \]
Der physikalische Grund für diese Drift ist wiederum die Änderung des Larmor-Radius, wenn das Teilchen im Gravitationsfeld Energie gewinnt und verliert. Jetzt drehen sich die Elektronen in die entgegengesetzte Richtung wie die Ionen, aber die Kraft, die auf sie einwirkt, geht in dieselbe Richtung, so dass die Drift in die entgegengesetzte Richtung geht. Die Größe von \(\mathbf{v}_g\) ist normalerweise vernachlässigbar, aber wenn die Kraftlinien (d.h. die Magnetfeldlinien) gekrümmt sind, gibt es eine effektive Gravitationskraft aufgrund der Zentrifugalkraft. Diese Kraft, die nicht vernachlässigbar ist, ist unabhängig von der Masse; aus diesem Grund haben wir die m-Abhängigkeit der Drift hier nicht betont. Die Zentrifugalkraft ist die Grundlage einer Plasmainstabilität, der so genannten “Gravitationsinstabilität”, die nichts mit der realen Schwerkraft zu tun hat.
function B(x)
return SA[0.0, 1e-8, 0.0]
end
function E(x)
return SA[0.0, 0.0, 0.0]
end
# gravity
function F(x)
return SA[0.0, 0.0, -TestParticle.mᵢ*9.8]
end
# initial static particle
x0 = [1.0, 0, 0]
v0 = [0.0, 0.0, 0.0]
stateinit = [x0..., v0...]
tspan = (0, 1.0)
param = prepare(E, B, F, species=Proton)
prob = ODEProblem(trace!, stateinit, tspan, param)
sol = solve(prob, Tsit5(); save_idxs=[1,2,3])
# drift in x-direction + free fall in z-direction
WM.plot(sol)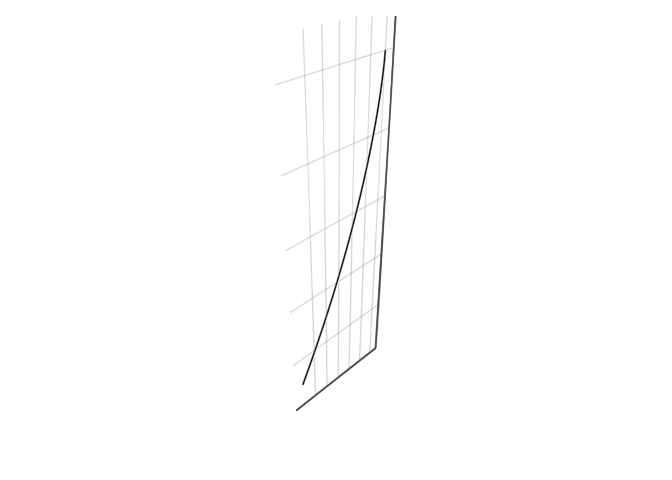
Da das Konzept der Drift des Führungszentrums nun fest etabliert ist, können wir die Bewegung von Teilchen in inhomogenen Feldern — \(\mathbf{E}\) und \(\mathbf{B}\) Feldern, die in Raum oder Zeit variieren, diskutieren. Für gleichförmige Felder konnten wir exakte Ausdrücke für die Drifts des Führungszentrums erhalten. Sobald wir Inhomogenität einführen, wird das Problem zu kompliziert, um es exakt zu lösen. Um eine ungefähre Antwort zu erhalten, ist es üblich, in dem kleinen Verhältnis \(r_L/L\) zu expandieren, wobei L die Skalenlänge der Inhomogenität ist. Diese Art von Theorie, die so genannte Orbit-Theorie, kann sehr kompliziert werden. Wir werden nur die einfachsten Fälle untersuchen, in denen jeweils nur eine Inhomogenität auftritt.
Hier sind die magnetischen Feldlinien nicht gekrümmt, aber ihre Dichte nimmt z. B. in y-Richtung zu. Wir können das Ergebnis vorhersagen, indem wir ein einfaches physikalisches Bild verwenden. Der Gradient in |B| bewirkt, dass der Larmor-Radius am unteren Ende der Bahn größer ist als am oberen Ende, und dies sollte zu einer Drift in entgegengesetzte Richtungen für Ionen und Elektronen führen, die sowohl senkrecht zu B als auch zu \(\nabla B\) verläuft. Die Driftgeschwindigkeit sollte offensichtlich proportional zu \(r_L/L\) und zu \(v_\perp\) sein.
Betrachten wir die Lorentz-Kraft \(\mathbf{F} = q\mathbf{v}\times\mathbf{B}\), gemittelt über eine Gyration. Es ist klar, dass \(\bar{F}_x = 0\) ist, da sich das Teilchen genauso viel Zeit nach oben wie nach unten bewegt. Wir wollen \(\bar{F}_y\) näherungsweise berechnen, indem wir die ungestörte Bahn des Teilchens verwenden, um den Durchschnitt zu finden. Die ungestörte Bahn ist durch die Lösung im ersten Abschnitt für ein gleichförmiges \(\mathbf{B}\)-Feld gegeben. Nimmt man den Realteil der Lösung für \(v_x\) und \(y\), so erhält man
\[ F_y = -q v_x B_z(y) = -q v_\perp(\cos \omega_c t) \Big[ B_0 \pm r_L(\cos\omega_c t )\frac{\partial B}{\partial y} \Big] \]
wobei wir eine Taylorentwicklung des Feldes \(\mathbf{B}\) um den Punkt \(x_0=0, y_0=0\) durchgeführt haben
\[ \begin{aligned} \mathbf{B} &= \mathbf{B}_0 + (\mathbf{r}\cdot\nabla)\mathbf{B} + ... \\ B_z &= B_0 + y(\partial B_z/\partial y) + ... \end{aligned} \]
Diese Entwicklung erfordert natürlich \(r_L / L \ll 1\), wobei L die Längenskala von \(\partial Bz/\partial y\) ist. Der erste obige Term geht bei einer Gyration im Durchschnitt gegen Null, und der Durchschnitt von \(\cos^2 \omega_c t\) ist \(1/2\), so dass
\[ \bar{F}_y = \mp q v_\perp r_L \frac{1}{2}\frac{\partial B}{\partial y} \]
Die Driftgeschwindigkeit des Führungszentrums beträgt dann
\[ \mathbf{v}_{gc} = \frac{1}{q}\frac{\mathbf{F}\times\mathbf{B}}{B^2} = \frac{1}{q}\frac{\bar{F}_y}{|B|}\widehat{x} = \mp \frac{v_\perp r_L}{B}\frac{1}{2} \frac{\partial B}{\partial y} \widehat{x} \]
wobei wir die zuvor gezeigte Formel verwendet haben. Da die Wahl der y-Achse willkürlich war, kann dies verallgemeinert werden zu
\[ \mathbf{v}_{\nabla B} = \pm v_\perp r_L \frac{\mathbf{B}\times \nabla B}{B^2} \]
Dies hat alle Abhängigkeiten, die wir aus dem physikalischen Bild erwartet haben; nur der Faktor \(\frac{1}{2}\) (der sich aus der Mittelwertbildung ergibt) wurde nicht vorhergesagt. Man beachte, dass \(\pm\) für das Vorzeichen der Ladung steht, und \(B\) für \(|B|\). Die Größe \(\mathbf{v}_{\nabla B}\) wird als Grad-B-Drift bezeichnet; sie verläuft für Ionen und Elektronen in entgegengesetzter Richtung und verursacht einen Strom quer zu \(\mathbf{B}\). Eine exakte Berechnung von \(\mathbf{v}_{\nabla B}\) würde die Verwendung der exakten Bahn, einschließlich der Drift, im Mittelungsprozess erfordern.
using ForwardDiff: gradient
function grad_B(x)
return SA[0, 0, 1e-8+1e-9 *x[2]]
end
function uniform_E(x)
return SA[1e-9, 0, 0]
end
abs_B(x) = norm(grad_B(x))
# trace the orbit of the guiding center
function trace_gc!(dx, x, p, t)
q, m, E, B, sol = p
xu = sol(t)
gradient_B = gradient(abs_B, x)
Bv = B(x)
b = normalize(Bv)
v_par = (xu[4:6]⋅b).*b
v_perp = xu[4:6] - v_par
dx[1:3] = m*norm(v_perp)^2*(Bv×gradient_B)/(2*q*norm(Bv)^3) + (E(x)×Bv)/norm(Bv)^2+v_par
end
x0 = [1.0, 0, 0]
v0 = [0.0, 1.0, 0.1]
stateinit = [x0..., v0...]
tspan = (0, 20)
param = prepare(uniform_E, grad_B, species=Proton)
prob = ODEProblem(trace!, stateinit, tspan, param)
sol = solve(prob, Tsit5(); save_idxs=[1,2,3,4,5,6])
gc = get_gc(param)
gc_x0 = [gc_i(stateinit) for gc_i in gc]
prob_gc = ODEProblem(trace_gc!, gc_x0, tspan, (param..., sol))
sol_gc = solve(prob_gc, Tsit5(); save_idxs=[1,2,3])
gc_analytic = Tuple(xu -> getindex(sol_gc(xu[7]), i) for i = 1:3)
# numeric result and analytic result
# The orbit of guiding center includes some high order terms, which is different from the
# formula of magnetic field gradient drift of some textbooks that just preserves the first
# order term.
orbit(sol, vars=[(1, 2, 3), gc, gc_analytic])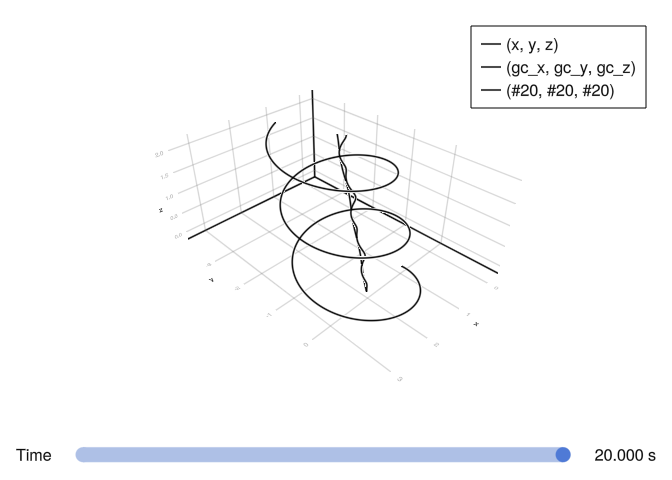
Hier nehmen wir an, dass die magnetischen Feldlinien mit einem konstanten Krümmungsradius \(R_c\) gekrümmt sind, und wir nehmen an, dass \(|B|\) konstant ist. Ein solches Feld gehorcht im Vakuum nicht den Maxwellschen Gleichungen, so dass in der Praxis die Grad-B-Drift immer zu dem hier abgeleiteten Effekt hinzukommt. Eine Drift des Führungszentrums entsteht durch die Zentrifugalkraft, die die Teilchen spüren, wenn sie sich bei ihrer thermischen Bewegung entlang der Feldlinien bewegen. Wenn \(v_\parallel^2\) das durchschnittliche Quadrat der Komponente der Zufallsgeschwindigkeit entlang \(\mathbf{B}\) bezeichnet, beträgt die durchschnittliche Zentrifugalkraft
\[ \mathbf{F}_{cf} = \frac{mv_\parallel^2}{R_c}\widehat{r} = mv_\parallel^2\frac{\mathbf{R}_c}{R_c^2} \]
Nach der Formel für die Drift des Führungszentrums ergibt sich daraus eine Drift
\[ \mathbf{v}_{R} = \frac{1}{q}\frac{\mathbf{F}_{cf}\times\mathbf{B}}{B^2} = \frac{mv_\parallel^2}{qB^2}\frac{\mathbf{R}_c \times\mathbf{B}}{R_c^2} \]
Die Drift \(\mathbf{v}_R\) wird als Krümmungsdrift bezeichnet.
Wir müssen nun die Grad-B-Drift berechnen, die damit einhergeht, wenn die Abnahme von \(|B|\) mit dem Radius berücksichtigt wird. Im Vakuum haben wir \(\nabla\times\mathbf{B} = 0\). In Zylinderkoordinaten hat \(\nabla\times\mathbf{B}\) nur eine \(z\)-Komponente, da \(\mathbf{B}\) nur eine \(\theta\)-Komponente und \(\nabla B\) nur eine \(r\)-Komponente hat. Wir haben dann
\[ (\nabla\times\mathbf{B})_z = \frac{1}{r}\frac{\partial}{\partial r}(rB_\theta) = 0,\, B\propto \frac{1}{r} \]
Deshalb
\[ |B| \propto \frac{1}{R_c},\, \frac{\nabla B}{B} = - \frac{\mathbf{R}_c}{R_c^2} \] Unter Verwendung des Ausdrucks für die Grad-B-Drift ergibt sich
\[ \mathbf{v}_{\nabla B} = \mp \frac{1}{2}\frac{v_\perp r_L}{B^2}\frac{B}\times |B| \frac{\mathbf{R}_c}{R_c^2} = \pm \frac{1}{2}\frac{v_\perp^2}{\omega_c}\frac{\mathbf{R}_c\times\mathbf{B}}{R_c^2 B} = \frac{1}{2}\frac{m}{q}v_\perp^2\frac{\mathbf{R}_c\times\mathbf{B}}{R_c^2 B^2} \]
Addiert man dies zu \(\mathbf{v}_R\) , so erhält man die Gesamtdrift in einem gekrümmten Vakuumfeld:
\[ \mathbf{v}_R + \mathbf{v}_{\nabla B} = \frac{m}{q}\frac{\mathbf{R}_c\times\mathbf{B}}{R_c^2 B^2}\Big( v_\parallel^2 + \frac{1}{2}v_\perp^2 \Big) \]
Bedauerlicherweise addieren sich diese Drifts. Das bedeutet, dass, wenn man ein Magnetfeld in einen Torus biegt, um ein thermonukleares Plasma einzuschließen, die Teilchen aus dem Torus herausdriften werden, egal wie man mit den Temperaturen und Magnetfeldern jongliert.
Für eine Maxwellsche Verteilung sind \(\bar{v_\parallel^2}\) und \(\frac{1}{2}\bar{v_\perp^2}\) jeweils gleich \(k_B T/m\), da \(v_\perp\) zwei Freiheitsgrade beinhaltet. Dann kann die durchschnittliche Drift des gekrümmten Feldes wie folgt geschrieben werden
\[ \bar{\mathbf{v}}_{R+\nabla B} = \pm \frac{v_{th}^2}{R_c\omega_c}\widehat{y} = \pm\frac{\bar{r}_L}{R_c}v_{th}\widehat{y} \]
wobei \(\widehat{y}\) hier die Richtung von \(\widehat{R}_c\times\mathbf{B}\) ist. Dies zeigt, dass \(\bar{\mathbf{v}}_{R+\nabla B}\) von der Ladung der Spezies abhängt, aber nicht von ihrer Masse.
using ForwardDiff: gradient, jacobian
function curved_B(x)
# satisify ∇⋅B=0
# B_θ = 1/r => ∂B_θ/∂θ = 0
θ = atan(x[3]/(x[1]+3))
r = hypot(x[1]+3, x[3])
return SA[-1e-7*sin(θ)/r, 0, 1e-7*cos(θ)/r]
end
function zero_E(x)
return SA[0, 0, 0]
end
abs_B(x) = norm(curved_B(x)) # |B|
# trace the orbit of the guiding center
function trace_gc!(dx, x, p, t)
q, m, E, B, sol = p
xu = sol(t)
gradient_B = gradient(abs_B, x) # ∇|B|
Bv = B(x)
b = normalize(Bv)
v_par = (xu[4:6]⋅b).*b # (v⋅b)b
v_perp = xu[4:6] - v_par
Ω = q*norm(Bv)/m
κ = jacobian(B, x)*Bv # B⋅∇B
# v⟂^2*(B×∇|B|)/(2*Ω*B^2) + v∥^2*(B×(B⋅∇B))/(Ω*B^3) + (E×B)/B^2 + v∥
dx[1:3] = norm(v_perp)^2*(Bv×gradient_B)/(2*Ω*norm(Bv)^2) +
norm(v_par)^2*(Bv×κ)/Ω/norm(Bv)^3 + (E(x)×Bv)/norm(Bv)^2 + v_par
end
x0 = [1.0, 0, 0]
v0 = [0.0, 1.0, 0.1]
stateinit = [x0..., v0...]
tspan = (0, 40)
# E×B drift
param = prepare(zero_E, curved_B, species=Proton)
prob = ODEProblem(trace!, stateinit, tspan, param)
sol = solve(prob, Tsit5(); save_idxs=[1,2,3,4,5,6])
gc = get_gc(param)
gc_x0 = [gc_i(stateinit) for gc_i in gc]
prob_gc = ODEProblem(trace_gc!, gc_x0, tspan, (param..., sol))
sol_gc = solve(prob_gc, Tsit5(); save_idxs=[1,2,3])
gc_analytic = Tuple(xu -> getindex(sol_gc(xu[7]), i) for i = 1:3)
# numeric result and analytic result
# similar to the magnetic field gradient drift
# analytic calculation should include both of the gradient drift and the curvature drift
orbit(sol, vars=[(1, 2, 3), gc, gc_analytic])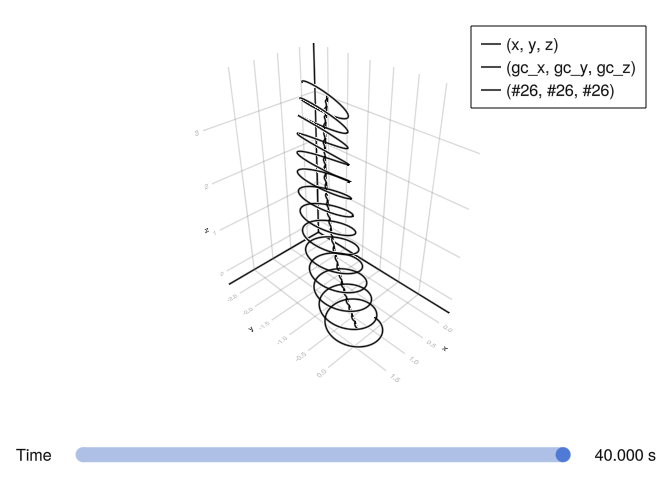
Wir betrachten nun ein Magnetfeld, das hauptsächlich in z-Richtung gerichtet ist und dessen Größe in z-Richtung variiert. Das Feld sei axialsymmetrisch, mit \(B_\theta = 0\) und \(\partial/\partial\theta = 0\). Da die Magnetfeldlinien konvergieren und divergieren, gibt es notwendigerweise eine Komponente \(B_r\). Wir wollen zeigen, dass daraus eine Kraft resultiert, die ein Teilchen in einem Magnetfeld einfangen kann.
Wir können \(B_r\) aus \(\nabla\cdot\mathbf{B} = 0\) erhalten:
\[ \frac{1}{r}\frac{\partial}{\partial r}(rB_r) + \frac{\partial B_z}{\partial z} = 0 \]
Wenn \(\mathbf{B}_z/\partial z\) bei \(r=0\) gegeben ist und nicht stark mit r variiert, haben wir ungefähr
\[ \begin{aligned} rB_r &= -\int_0^r r\frac{\partial B_z}{\partial z}dr \simeq -\frac{1}{2}r^2 \Big[ \frac{\partial \mathbf{B}_z}{\partial z} \Big]_{r=0} \\ B_r &= -\frac{1}{2}r \Big[ \frac{\partial \mathbf{B}_z}{\partial z} \Big]_{r=0} \end{aligned} \]
Die Variation von \(|B|\) mit r bewirkt eine grad-B-Drift der Führungszentren um die Symmetrieachse, aber es gibt keine radiale grad-B-Drift, weil \(\partial B/\partial \theta = 0\). Die Komponenten der Lorentzkraft sind
\[ \newcommand{\textcircled}[1]{\enclose{circle}{\kern.1em\text{#1}\kern.1em}} \begin{aligned} F_r &= q(\underbrace{v_\theta B_z}_{\textcircled{\small{1}}} - v_z \cancel{B_\theta}) \\ F_\theta &= q(\underbrace{-v_r B_z}_{\textcircled{\small{2}}} + \underbrace{v_z B_r}_{\textcircled{\small{3}}}) \\ F_z &= q(v_r \cancel{B}_\theta - \underbrace{v_\theta B_r}_{\textcircled{\small{4}}}) \end{aligned} \]
Zwei Terme verschwinden, wenn \(B_\theta = 0\) ist, und die Terme 1 und 2 bewirken die übliche Larmor-Gyration. Term 3 verschwindet auf der Achse; wenn er nicht verschwindet, verursacht diese azimutale Kraft eine Drift in radialer Richtung. Diese Drift führt lediglich dazu, dass die Führungszentren den Magnetfeldlinien folgen. Term 4 ist derjenige, für den wir uns interessieren. Unter Verwendung des Ausdrucks für \(B_r\) ergibt sich
\[ F_z = \frac{1}{2}q v_\theta r_L \frac{\partial B_z}{\partial z} \]
Wir müssen nun den Durchschnitt über eine Gyration bilden. Der Einfachheit halber betrachten wir ein Teilchen, dessen Führungszentrum auf der Achse liegt. Dann ist \(v_\theta\) eine Konstante während einer Gyration; je nach Vorzeichen von q ist \(v_\theta\) gleich \(\mp v_\perp\). Da \(r = r_L\) , ist die mittlere Kraft
\[ \bar{F}_z = \mp \frac{1}{2}q v_\perp r_L \frac{\partial B_z}{\partial z} = \mp \frac{1}{2}q\frac{v_\perp^2}{\omega_c} \frac{\partial B_z}{\partial z} = -\frac{1}{2}\frac{mv_\perp^2}{B} \frac{\partial B_z}{\partial z} \]
Wir definieren das magnetische Moment des kreisenden Teilchens wie folgt
\[ \mu \equiv \frac{1}{2}mv_\perp^2 / B \]
so dass
\[ \bar{F}_z = -\mu \frac{\partial B_z}{\partial z} \]
Dies ist ein spezifisches Beispiel für die Kraft, die auf ein diamagnetisches Teilchen einwirkt und die sich im Allgemeinen wie folgt berechnen lässt
\[ \mathbf{F}_\parallel = -\mu\frac{\partial B}{\partial \mathbf{s}} = -\mu\nabla_\parallel B \]
wobei \(d\mathbf{s}\) ein Linienelement entlang \(\mathbf{B}\) ist. Man beachte, dass die Definition des magnetischen Moments hier dieselbe ist wie die übliche Definition für das magnetische Moment einer Stromschleife mit der Fläche A und dem Strom I: \(\mu = IA\). Im Falle eines einfach geladenen Ions wird I durch eine Ladung e erzeugt, die \(\omega_c / 2\pi\) mal pro Sekunde umläuft: \(I = e\omega_c/2\pi\). Die Fläche A ist \(\pi r_L^2 = \pi r_L^2/\omega_c^2\). Also
\[ \mu = \frac{e\omega_c}{2\pi}\frac{\pi r_L^2}{\omega_c^2} = \frac{1}{2}\frac{v_\perp^2 e}{\omega_c} = \frac{1}{2}\frac{mv_\perp^2}{B} \]
Wenn sich das Teilchen in Regionen mit stärkerem oder schwächerem B bewegt, ändert sich sein Larmor-Radius, aber μ bleibt invariant. Um dies zu beweisen, betrachten wir die Komponente der Bewegungsgleichung entlang \(\mathbf{B}\):
\[ m\frac{dv_\parallel}{dt} = -\mu \frac{\partial B}{\partial s} \]
Durch Multiplikation mit \(v_\parallel\) auf der linken Seite und seinem Äquivalent \(ds/dt\) auf der rechten Seite erhalten wir
\[ mv_\parallel \frac{dv_\parallel}{dt} = \frac{d}{dt}\Big( \frac{1}{2}mv_\parallel^2 \Big) = -\mu\frac{\partial B}{\partial s}\frac{ds}{dt} = -\mu\frac{dB}{dt} \]
Dabei ist dB/dt die Veränderung von B aus der Sicht des Teilchens; B selbst ist konstant. Die Energie des Teilchens muss erhalten bleiben, also gilt
\[ \frac{d}{dt}\Big( \frac{1}{2}mv_\parallel^2 + \frac{1}{2}mv_\perp^2 \Big) = \frac{d}{dt}\Big( \frac{1}{2}mv_\parallel^2 + \mu B \Big) = 0 \]
Mit der vorhergehenden Gleichung ergibt sich
\[ -\mu\frac{dB}{dt} + \frac{d}{dt}(\mu B) = 0 \]
so dass
\[ \frac{d\mu}{dt} = 0 \]
Die Invarianz von \(\mu\) ist die Grundlage für eines der wichtigsten Systeme für den Plasmaeinschluss: den magnetischen Spiegel. Wenn sich ein Teilchen im Laufe seiner thermischen Bewegung von einem Bereich mit schwachem Feld zu einem Bereich mit starkem Feld bewegt, sieht es ein zunehmendes B, und daher muss sein \(v_\perp\) zunehmen, um μ konstant zu halten. Da seine Gesamtenergie konstant bleiben muss, muss \(v_\parallel\) zwangsläufig abnehmen. Wenn B in der “Kehle” des Spiegels hoch genug ist, wird \(v_\parallel\) schließlich zu Null; und das Teilchen wird in den Bereich des schwachen Feldes “zurückgeworfen”. Es ist natürlich die Kraft \(\mathbf{F}_\parallel\), die die Reflexion verursacht. Das ungleichmäßige Feld eines einfachen Spulenpaares bildet zwei Magnetspiegel, zwischen denen ein Plasma gefangen werden kann. Dieser Effekt funktioniert sowohl bei Ionen als auch bei Elektronen.
Das Einfangen ist jedoch nicht perfekt. Ein Teilchen mit \(v_\perp = 0\) hat zum Beispiel kein magnetisches Moment und spürt keine Kraft entlang \(\mathbf{B}\). Ein Teilchen mit kleinem \(v_\perp / v_\parallel\) in der Mittelebene (\(B = B_0\)) wird ebenfalls entkommen, wenn das maximale Feld \(B_m\) nicht groß genug ist. Welche Teilchen werden bei gegebenem \(B_0\) und \(B_m\) entkommen? Ein Teilchen mit \(v_\perp = v_{\perp 0}\) und \(v_\parallel = v_{\parallel 0}\) in der Mittelebene hat \(v_\perp = v_\perp^\prime\) und \(v_\parallel = 0\) an seinem Wendepunkt. Das Feld sei dort \(B^\prime\). Dann ergibt die Invariante von \(\mu\)
\[ \frac{1}{2}\frac{mv_{\perp 0}^2}{B_0} = \frac{1}{2}\frac{m{v_{\perp 0}^{\prime}}^2}{B^\prime} \]
Die Energieerhaltung erfordert
\[ {v_{\perp 0}^{\prime}}^2 = v_{\perp 0}^2 + v_{\parallel 0}^2 \equiv v_0^2 \]
Kombiniert man die beiden obigen Gleichungen, erhält man
\[ \frac{B_0}{B^\prime} = \frac{v_{\perp 0}^2}{{v_{\perp}^{\prime}}^2} \equiv \sin^2 \theta \]
wobei \(\theta\) der Neigungswinkel der Bahn im Bereich des schwachen Feldes ist. Teilchen mit kleinerem θ spiegeln sich in Regionen mit höherem B. Wenn θ zu klein ist, übersteigt \(B^\prime\) \(B_m\), und das Teilchen spiegelt sich überhaupt nicht. Ersetzt man \(B^\prime\) durch \(B_m\), so sieht man, dass die kleinste \(\theta\) eines eingeschlossenen Teilchens gegeben ist durch
\[ \sin^2 \theta_m = \frac{B_0}{B_m} \equiv \frac{1}{R_m} \]
wobei \(R_m\) das Spiegelverhältnis ist. Es definiert die Grenze eines Bereichs im Geschwindigkeitsraum in Form eines Kegels, der Verlustkegel genannt wird. Teilchen, die sich innerhalb des Verlustkegels befinden, sind nicht eingegrenzt. Folglich ist ein spiegelbegrenztes Plasma niemals isotrop. Beachten Sie, dass der Verlustkegel unabhängig von q oder m ist. Ohne Kollisionen sind Ionen und Elektronen gleich gut eingeschlossen. Wenn es zu Kollisionen kommt, gehen Teilchen verloren, wenn sie bei einer Kollision ihren Neigungswinkel ändern und in den Verlustkegel gestreut werden. Im Allgemeinen gehen Elektronen leichter verloren, da sie eine höhere Kollisionsfrequenz haben.
Der Magnetspiegel wurde erstmals von Enrico Fermi als Mechanismus für die Beschleunigung der kosmischen Strahlung vorgeschlagen. Protonen, die zwischen magnetischen Spiegeln abprallen und sich mit hoher Geschwindigkeit aufeinander zubewegen, könnten bei jedem Aufprall Energie gewinnen. Wie solche Spiegel entstehen können, ist eine andere Geschichte. Ein weiteres Beispiel für den Spiegeleffekt ist der Einschluss von Teilchen in den Van-Allen-Gürteln. Das Magnetfeld der Erde, das an den Polen stark und am Äquator schwach ist, bildet einen natürlichen Spiegel mit ziemlich großem \(R_m\).
Aöllgemeine Kraft:
\[ \mathbf{v}_f = \frac{1}{q}\frac{\mathbf{F}\times\mathbf{B}}{B^2} \]
E-Feld:
\[ \mathbf{v}_E = \frac{\mathbf{E}\times\mathbf{B}}{B^2} \]
Gravitation:
\[ \mathbf{v}_g = \frac{m}{q}\frac{\mathbf{g}\times\mathbf{B}}{B^2} \]
Inhomogenes elektrisches Feld:
\[ \mathbf{v}_E = \Big( 1+\frac{1}{4}r_L^2 \nabla^2 \Big)\frac{\mathbf{E}\times\mathbf{B}}{B^2} \]
Inhomogenes Magnetfeld:
Grad-B:
\[ \mathbf{v}_{\nabla B} = \pm \frac{1}{2}v_\perp r_L\frac{\mathbf{B}\times\nabla B}{B^2} \]
Krümmungsdrift:
\[ \mathbf{v}_R = \frac{mv_\parallel^2}{q}\frac{\mathbf{R}_c \times\mathbf{B}}{R_c^2 B^2} \]
Gekrümmte Feldlinie:
\[ \mathbf{v}_R + \mathbf{v}_{\nabla B} = \frac{m}{q}\Big( v_\parallel^2 + \frac{1}{2}v_\perp^2 \Big) \frac{\mathbf{R}_c \times\mathbf{B}}{R_c^2 B^2} \]
Polarsationsdrift:
\[ \mathbf{v}_p = \pm \frac{1}{\omega_c B}\frac{d\mathbf{E}}{dt} \]